Metabolic Dynamics of Ecosystems Realizing Steady Log-Uniform Distributions: The Case of Commodities in Shops
Abstract
:1. Introduction
2. Materials
3. Results
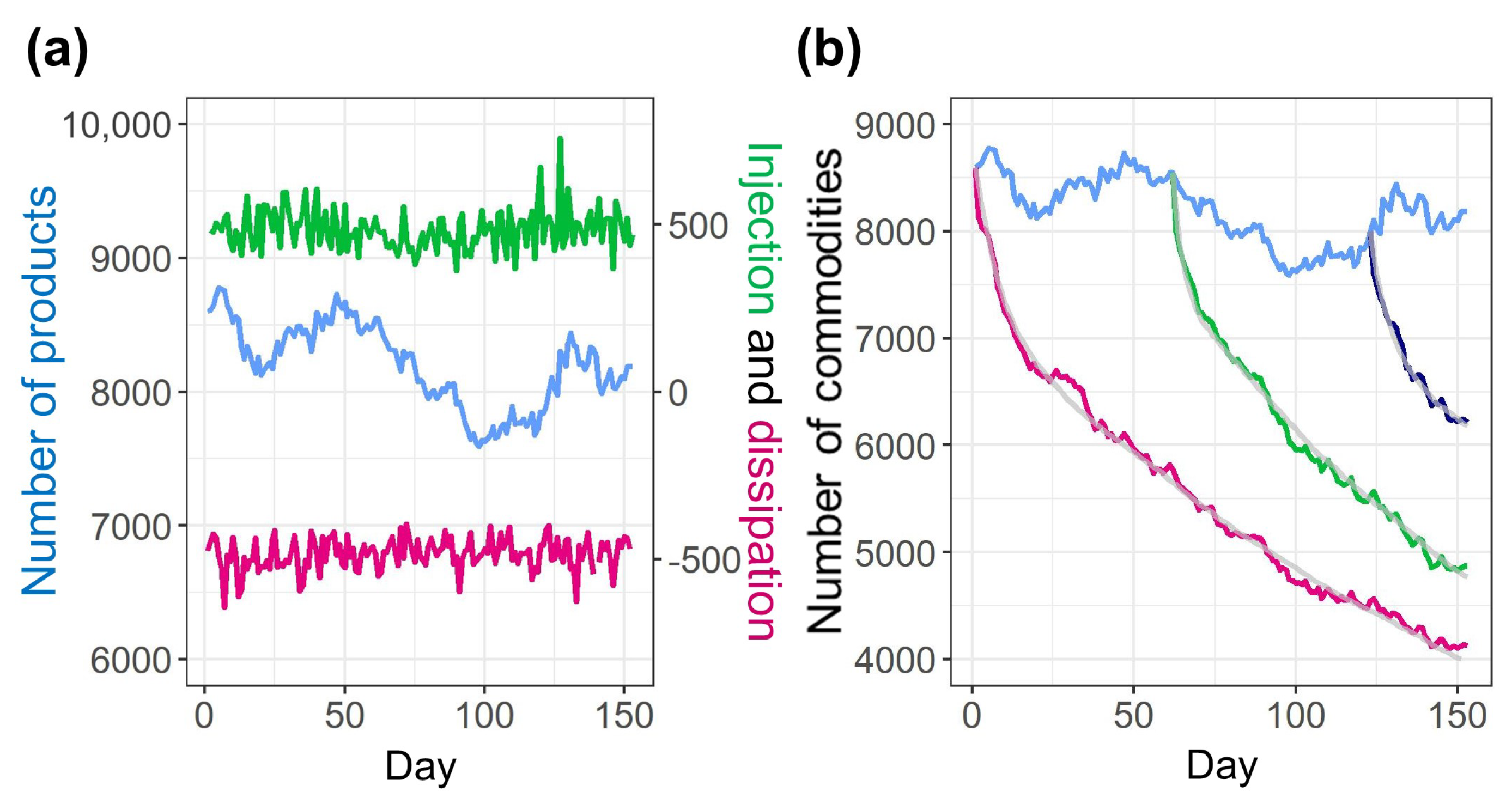
3.1. Metabolism of Commodity Species
3.2. Log-Uniform Distribution
3.3. Dynamics of the Log-Uniform Distribution
3.4. Random Multiplicative Diffusion Simulation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Newman, M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323. [Google Scholar] [CrossRef] [Green Version]
- Smoluchowski, M.V. Drei vortrage uber diffusion, Brownsche beregund und koagulation von kolloidteilchen. Zeitschrift für Physik 1916, 17, 585. [Google Scholar]
- Takayasu, H. Steady-state distribution of generalized aggregation system with injection. Phys. Rev. Lett. 1989, 63, 2563. [Google Scholar] [CrossRef]
- Takayasu, M. Universal power law observed in an exponentially growing particle system. Phys. Rev. A. 1992, 46, 782. [Google Scholar] [CrossRef]
- Takayasu, H.; Taguchi, Y.-h. Non-Gaussian distribution in random advection dynamics. Phys. Rev. Lett. 1993, 70, 782. [Google Scholar] [CrossRef] [Green Version]
- Takayasu, M.; Takayasu, H.; Taguchi, Y.-h. Non-Gaussian distribution in random transport dynamics. Int. J. Mod. Phys. B 1994, 8, 3887. [Google Scholar] [CrossRef] [Green Version]
- Krapivsky, P.L.; Redner, S. Transitional aggregation kinetics in dry and damp environments. Phys. Rev. E 1996, 54, 3553. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedlander, S.K. Smoke, Dust, and Haze: Fundamentals of Aerosol Dynamics, 2nd ed.; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory Rev., 2nd ed.; Taylor & Francis: London, UK, 1994. [Google Scholar]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 1987, 59, 381. [Google Scholar] [CrossRef] [PubMed]
- Lu, E.T.; Hamilton, R.J. Avalanches and the Distribution of Solar Flares. Astrophys. J. 1991, 380, 89. [Google Scholar] [CrossRef]
- Olami, Z.; Feder, H.J.S.; Christensen, K. Self-organized criticality in a continuous, nonconservative cellular automaton modeling earthquakes. Phys. Rev. Lett. 1992, 68, 1244. [Google Scholar] [CrossRef] [Green Version]
- Bak, P.; Sneppen, K. Punctuated equilibrium and criticality in a simple model of evolution. Phys. Rev. Lett. 1993, 71, 4083. [Google Scholar] [CrossRef] [PubMed]
- Mizuno, T.; Kurihara, S.; Takayasu, M.; Takayasu, H. Analysis of high-resolution foreign exchange data of USD-JPY for 13 years. Physica A 2003, 324, 296. [Google Scholar] [CrossRef] [Green Version]
- Okuyama, K.; Takayasu, M.; Takayasu, H. Zipf’s law in income distribution of companies. Physica A 1999, 269, 125. [Google Scholar] [CrossRef]
- Miura, W.; Takayasu, H.; Takayasu, M. Effect of Coagulation of Nodes in an Evolving Complex Network. Phys. Rev. Lett. 2012, 108, 168701. [Google Scholar] [CrossRef] [Green Version]
- Yule, G.U. II.—A mathematical theory of evolution, based on the conclusions of Dr. J. C. Willis, F. R. S. Phil. Trans. R. Soc. Lond. B 1925, 213, 21. [Google Scholar]
- Simon, H.A. On a Class of Skew Distribution Functions. Biometrika 1955, 42, 425. [Google Scholar] [CrossRef]
- Barabási, R.; Albert, A. Emergence of Scaling in Random Networks. Science 1999, 286, 509. [Google Scholar] [CrossRef] [Green Version]
- Feller, W. An Introduction to Probability Theory and Its Applications; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Levy, M.; Solomon, S. Power laws are logarithmic Boltzmann laws. Int. J. Mod. Phys. C. 1996, 7, 595. [Google Scholar] [CrossRef] [Green Version]
- Takayasu, H.; Sato, A.H.; Takayasu, M. Stable Infinite Variance Fluctuations in Randomly Amplified Langevin Systems. Phys. Rev. Lett. 1997, 79, 966. [Google Scholar] [CrossRef]
- Meeker, W.Q.; Hahn, G.J.; Escobar, L.A. Statistical Intervals: A Guide for Practitioners and Researchers; Wiley: New York, NY, USA, 2017. [Google Scholar]
- Suzuki, M.; Oshima, T. Co-ordination number of a multi-component randomly packed bed of spheres with size distribution. Powder Technol. 1985, 44, 213. [Google Scholar] [CrossRef]
- Connelley, M.S.; Reipurth, B.; Tokunaga, A.T. The Evolution of the Multiplicity of Embedded Protostars II: Binary Separation Distribution & Analysis. Astron. J. 2008, 135, 2526. [Google Scholar]
- Rabeaud, O.; Royer, J.J.; Jébrak, M.; Cheilletz, A. Log-uniform distribution of gold deposits along major Archean fault zones. Miner. Depos. 2013, 48, 817. [Google Scholar] [CrossRef]
- Tsafrir, D.; Etsion, Y.; Feitelson, D.G. Modeling User Runtime Estimates. Job Sched. Strateg. Parallel Process. 2005, 3834, 1. [Google Scholar]
- Seven & i Holdings Co., Ltd. Corporate Outline 2011. Available online: https://www.7andi.com/library/dbps_data/_template_/_res/en/ir/library/co/pdf/2011_07.pdf (accessed on 8 February 2020).



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakoda, G.; Takayasu, H.; Takayasu, M. Metabolic Dynamics of Ecosystems Realizing Steady Log-Uniform Distributions: The Case of Commodities in Shops. Entropy 2020, 22, 267. https://doi.org/10.3390/e22030267
Sakoda G, Takayasu H, Takayasu M. Metabolic Dynamics of Ecosystems Realizing Steady Log-Uniform Distributions: The Case of Commodities in Shops. Entropy. 2020; 22(3):267. https://doi.org/10.3390/e22030267
Chicago/Turabian StyleSakoda, Gen, Hideki Takayasu, and Misako Takayasu. 2020. "Metabolic Dynamics of Ecosystems Realizing Steady Log-Uniform Distributions: The Case of Commodities in Shops" Entropy 22, no. 3: 267. https://doi.org/10.3390/e22030267
APA StyleSakoda, G., Takayasu, H., & Takayasu, M. (2020). Metabolic Dynamics of Ecosystems Realizing Steady Log-Uniform Distributions: The Case of Commodities in Shops. Entropy, 22(3), 267. https://doi.org/10.3390/e22030267





